Imposing an interaface condition in Poisson problem, serial version. More...

#include <poisson_nitsche_interface.h>

Inheritance diagram for PDEs::Serial::PoissonNitscheInterface< dim, spacedim >:

Public Member Functions
	PoissonNitscheInterface ()

void	run ()

Public Member Functions inherited from ParameterAcceptor
	ParameterAcceptor (const std::string &section_name="")

unsigned int	get_acceptor_id () const

virtual	~ParameterAcceptor () override

virtual void	declare_parameters (ParameterHandler &prm)

virtual void	parse_parameters (ParameterHandler &prm)

std::string	get_section_name () const

std::vector< std::string >	get_section_path () const

void	add_parameter (const std::string &entry, ParameterType &parameter, const std::string &documentation="", ParameterHandler &prm_=prm, const Patterns::PatternBase &pattern=*Patterns::Tools::Convert< ParameterType >::to_pattern())

void	enter_subsection (const std::string &subsection)

void	leave_subsection ()

void	enter_my_subsection (ParameterHandler &prm)

void	leave_my_subsection (ParameterHandler &prm)

void	serialize (Archive &ar, const unsigned int version)

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

Public Member Functions inherited from Subscriptor
	Subscriptor ()

	Subscriptor (const Subscriptor &)

	Subscriptor (Subscriptor &&) noexcept

virtual	~Subscriptor ()

Subscriptor &	operator= (const Subscriptor &)

Subscriptor &	operator= (Subscriptor &&) noexcept

void	serialize (Archive &ar, const unsigned int version)

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

Protected Member Functions
void	generate_grids ()

void	setup_system ()
	Setup dofs, constraints, and matrices. More...

void	assemble_system ()

void	solve ()

void	output_results (const unsigned cycle) const

Protected Attributes
const std::string	component_names = "u"

ParsedTools::GridGenerator< spacedim, spacedim >	grid_generator

ParsedTools::GridGenerator< dim, spacedim >	embedded_grid_generator

ParsedTools::GridRefinement	grid_refinement

Triangulation< spacedim, spacedim >	space_triangulation
	The actual triangulations. More...

Triangulation< dim, spacedim >	embedded_triangulation

std::unique_ptr< GridTools::Cache< spacedim, spacedim > >	space_cache
	GridTools::Cache objects are used to cache all the necessary information about a given triangulation, such as its Mapping, Bounding Boxes, etc. More...

std::unique_ptr< GridTools::Cache< dim, spacedim > >	embedded_cache

std::vector< std::tuple< typename Triangulation< spacedim, spacedim >::cell_iterator, typename Triangulation< dim, spacedim >::cell_iterator, Quadrature< spacedim > > >	cells_and_quads
	The coupling between the two grids is ultimately encoded in this vector. More...

ParsedTools::FiniteElement< spacedim, spacedim >	space_fe

DoFHandler< spacedim, spacedim >	space_dh
	The actual DoFHandler class. More...

std::unique_ptr< Mapping< spacedim, spacedim > >	mapping
	According to the Triangulation type, we use a MappingFE or a MappingQ, to make sure we can run the program both on a tria/tetra grid and on quad/hex grids. More...

Linear algebra classes
AffineConstraints< double >	space_constraints

SparsityPattern	sparsity_pattern

SparseMatrix< double >	system_matrix

Vector< double >	solution

Vector< double >	system_rhs

ParsedLAC::InverseOperator	inverse_operator

ParsedLAC::AMGPreconditioner	preconditioner

Forcing terms and boundary conditions
ParsedTools::Constants	constants

ParsedTools::Function< spacedim >	forcing_term
	The actual function to use as a forcing term. More...

ParsedTools::Function< spacedim >	embedded_value
	This is the value we want to impose on the embedded domain. More...

ParsedTools::Function< spacedim >	nitsche_coefficient
	The coefficient in front of the Nitsche contribution to the stiffness matrix. More...

ParsedTools::Function< spacedim >	exact_solution
	The actual function to use as a exact solution when computing the errors. More...

ParsedTools::BoundaryConditions< spacedim >	boundary_conditions

Output and postprocessing
TimerOutput	timer

ParsedTools::ConvergenceTable	error_table

ParsedTools::DataOut< spacedim, spacedim >	data_out
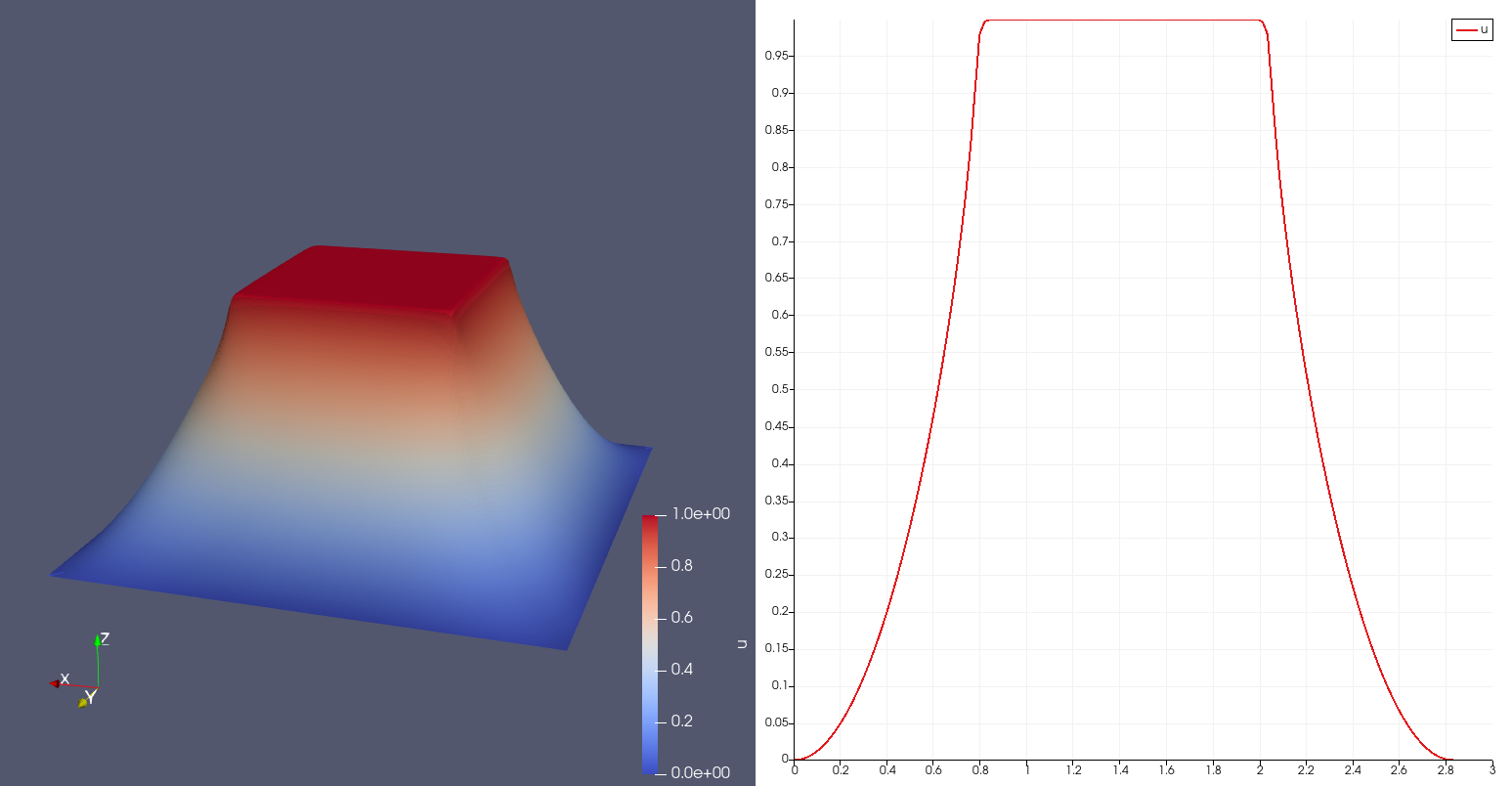
	Choosing as embedded space the square \([-.0.45,0.45]^2\) and as embedding space the square \([-1,1]^2\), with embedded value the function \(g(x,y)=1\), this is what we get. More...

unsigned int	console_level = 1
	Level of log verbosity. More...

double	penalty = 100.0
	The penalty parameter which multiplies Nitsche's terms. More...

Protected Attributes inherited from ParameterAcceptor
const std::string	section_name

std::vector< std::string >	subsections

Additional Inherited Members
Static Public Member Functions inherited from ParameterAcceptor
static void	initialize (const std::string &filename="", const std::string &output_filename="", const ParameterHandler::OutputStyle output_style_for_output_filename=ParameterHandler::Short, ParameterHandler &prm=ParameterAcceptor::prm, const ParameterHandler::OutputStyle output_style_for_filename=ParameterHandler::DefaultStyle)

static void	initialize (std::istream &input_stream, ParameterHandler &prm=ParameterAcceptor::prm)

static void	clear ()

static void	parse_all_parameters (ParameterHandler &prm=ParameterAcceptor::prm)

static void	declare_all_parameters (ParameterHandler &prm=ParameterAcceptor::prm)

static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)

static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)

Static Public Member Functions inherited from Subscriptor
static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)

static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)

Public Attributes inherited from ParameterAcceptor
boost::signals2::signal< void()>	declare_parameters_call_back

boost::signals2::signal< void()>	parse_parameters_call_back

Static Public Attributes inherited from ParameterAcceptor
static ParameterHandler	prm

Detailed Description

template<int dim, int spacedim = dim>
class PDEs::Serial::PoissonNitscheInterface< dim, spacedim >

Imposing an interaface condition in Poisson problem, serial version.

Here we solve the Poisson equation:

\[ \begin{cases} - \Delta u = f & \text{ in } \Omega \subset R^{\text{spacedim}}\\ u = u_D = 0 & \text{ on } \partial \Omega \\ u = g & \text{on} B \\ \end{cases} \]

where B is a domain embedded in \Omega. The structure of the program is the usual one, what really changes is the weak form. To get that, we apply Nitsche's method in \(\Omega \setminus B\) and \(B\), separately, as done in step-70 tutorial. For an extended discussion see there and references therein. All in all, what one gets using Lagrangian finite elements in codimension 1 is to find \(u \in H_0^1(\Omega)\) s.t.

\begin{align*} (\nabla u, \nabla v) + 2 \beta \langle u,v \rangle_{\Gamma} =(f,v) + 2 \beta \langle g,v \rangle_{\Gamma} \end{align*}

for all test functions \(v \in H_0^1(\Omega)\). Here \(\Gamma = \partial B\) in codimension 1. The contributions from Nitsche's method then have to be added both to the stiffness matrix and to the right hand side. The thing here is that they have to be computed on the embedded grid, while \(u\) and \(v\) live on the ambient space.

Definition at line 107 of file poisson_nitsche_interface.h.

Constructor & Destructor Documentation

◆ PoissonNitscheInterface()

template<int dim, int spacedim>

PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::PoissonNitscheInterface

Definition at line 31 of file poisson_nitsche_interface.cc.

Member Function Documentation

◆ run()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::run

Definition at line 282 of file poisson_nitsche_interface.cc.

References deallog, LogStream::depth_console(), Utilities::int_to_string(), LogStream::pop(), and LogStream::push().

◆ generate_grids()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::generate_grids

protected

Definition at line 70 of file poisson_nitsche_interface.cc.

◆ setup_system()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::setup_system

protected

Setup dofs, constraints, and matrices.

This function enumerate all the degrees of freedom and set up matrix and vector objects to hold the system data. Enumerating is done by using DoFHandler::distribute_dofs(), as we have seen in the step-2 example, with the difference that now we pass a ParsedTools::FiniteElement object instead of directly a FiniteElement object.

Definition at line 88 of file poisson_nitsche_interface.cc.

References AssertThrow, deallog, StandardExceptions::ExcMessage(), get_default_linear_mapping(), DoFTools::make_hanging_node_constraints(), DoFTools::make_sparsity_pattern(), and reference_cell().

◆ assemble_system()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::assemble_system

protected

Definition at line 141 of file poisson_nitsche_interface.cc.

References deallog, ReferenceCell::get_gauss_type_quadrature(), update_gradients, update_JxW_values, update_quadrature_points, and update_values.

◆ solve()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::solve

protected

Definition at line 238 of file poisson_nitsche_interface.cc.

References deallog, and inverse_operator().

◆ output_results()

template<int dim, int spacedim>

void PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::output_results ( const unsigned cycle ) const

protected

Definition at line 255 of file poisson_nitsche_interface.cc.

References deallog, Utilities::int_to_string(), Utilities::needed_digits(), and GridOut::write_vtk().

Member Data Documentation

◆ component_names

template<int dim, int spacedim = dim>

const std::string PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::component_names = "u"

protected

Definition at line 148 of file poisson_nitsche_interface.h.

◆ grid_generator

template<int dim, int spacedim = dim>

ParsedTools::GridGenerator<spacedim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::grid_generator

protected

Definition at line 151 of file poisson_nitsche_interface.h.

◆ embedded_grid_generator

template<int dim, int spacedim = dim>

ParsedTools::GridGenerator<dim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::embedded_grid_generator

protected

Definition at line 153 of file poisson_nitsche_interface.h.

◆ grid_refinement

template<int dim, int spacedim = dim>

ParsedTools::GridRefinement PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::grid_refinement

protected

Definition at line 155 of file poisson_nitsche_interface.h.

◆ space_triangulation

template<int dim, int spacedim = dim>

Triangulation<spacedim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::space_triangulation

protected

The actual triangulations.

Here with "space_triangulation" we refer to the original domain \Omega, also called the ambient space, while with embedded we refer to the immersed domain, the one where we want to impose a constraint.

Definition at line 164 of file poisson_nitsche_interface.h.

◆ embedded_triangulation

template<int dim, int spacedim = dim>

Triangulation<dim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::embedded_triangulation

protected

Definition at line 165 of file poisson_nitsche_interface.h.

◆ space_cache

template<int dim, int spacedim = dim>

std::unique_ptr<GridTools::Cache<spacedim, spacedim> > PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::space_cache

protected

GridTools::Cache objects are used to cache all the necessary information about a given triangulation, such as its Mapping, Bounding Boxes, etc.

Definition at line 173 of file poisson_nitsche_interface.h.

◆ embedded_cache

template<int dim, int spacedim = dim>

std::unique_ptr<GridTools::Cache<dim, spacedim> > PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::embedded_cache

protected

Definition at line 174 of file poisson_nitsche_interface.h.

◆ cells_and_quads

template<int dim, int spacedim = dim>

std::vector<std::tuple< typename Triangulation<spacedim, spacedim>::cell_iterator, typename Triangulation<dim, spacedim>::cell_iterator, Quadrature<spacedim> > > PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::cells_and_quads

protected

The coupling between the two grids is ultimately encoded in this vector.

Here the i-th entry stores a tuple for which the first two elements are iterators to two cells from the space and embedded grid, respectively, that intersect each other (up to a specified tolerance) and a Quadrature object to integrate over that region.

Definition at line 189 of file poisson_nitsche_interface.h.

◆ space_fe

template<int dim, int spacedim = dim>

ParsedTools::FiniteElement<spacedim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::space_fe

protected

Definition at line 192 of file poisson_nitsche_interface.h.

◆ space_dh

template<int dim, int spacedim = dim>

DoFHandler<spacedim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::space_dh

protected

The actual DoFHandler class.

Definition at line 197 of file poisson_nitsche_interface.h.

◆ mapping

template<int dim, int spacedim = dim>

std::unique_ptr<Mapping<spacedim, spacedim> > PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::mapping

protected

According to the Triangulation type, we use a MappingFE or a MappingQ, to make sure we can run the program both on a tria/tetra grid and on quad/hex grids.

Definition at line 204 of file poisson_nitsche_interface.h.

◆ space_constraints

template<int dim, int spacedim = dim>

AffineConstraints<double> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::space_constraints

protected

Definition at line 211 of file poisson_nitsche_interface.h.

◆ sparsity_pattern

template<int dim, int spacedim = dim>

SparsityPattern PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::sparsity_pattern

protected

Definition at line 212 of file poisson_nitsche_interface.h.

◆ system_matrix

template<int dim, int spacedim = dim>

SparseMatrix<double> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::system_matrix

protected

Definition at line 213 of file poisson_nitsche_interface.h.

◆ solution

template<int dim, int spacedim = dim>

Vector<double> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::solution

protected

Definition at line 214 of file poisson_nitsche_interface.h.

◆ system_rhs

template<int dim, int spacedim = dim>

Vector<double> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::system_rhs

protected

Definition at line 215 of file poisson_nitsche_interface.h.

◆ inverse_operator

template<int dim, int spacedim = dim>

ParsedLAC::InverseOperator PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::inverse_operator

protected

Definition at line 216 of file poisson_nitsche_interface.h.

◆ preconditioner

template<int dim, int spacedim = dim>

ParsedLAC::AMGPreconditioner PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::preconditioner

protected

Definition at line 217 of file poisson_nitsche_interface.h.

◆ constants

template<int dim, int spacedim = dim>

ParsedTools::Constants PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::constants

protected

Definition at line 226 of file poisson_nitsche_interface.h.

◆ forcing_term

template<int dim, int spacedim = dim>

ParsedTools::Function<spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::forcing_term

protected

The actual function to use as a forcing term.

Definition at line 231 of file poisson_nitsche_interface.h.

◆ embedded_value

template<int dim, int spacedim = dim>

ParsedTools::Function<spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::embedded_value

protected

This is the value we want to impose on the embedded domain.

Definition at line 238 of file poisson_nitsche_interface.h.

◆ nitsche_coefficient

template<int dim, int spacedim = dim>

ParsedTools::Function<spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::nitsche_coefficient

protected

The coefficient in front of the Nitsche contribution to the stiffness matrix.

Definition at line 246 of file poisson_nitsche_interface.h.

◆ exact_solution

template<int dim, int spacedim = dim>

ParsedTools::Function<spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::exact_solution

protected

The actual function to use as a exact solution when computing the errors.

Definition at line 252 of file poisson_nitsche_interface.h.

◆ boundary_conditions

template<int dim, int spacedim = dim>

ParsedTools::BoundaryConditions<spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::boundary_conditions

protected

Definition at line 255 of file poisson_nitsche_interface.h.

◆ timer

template<int dim, int spacedim = dim>

TimerOutput PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::timer

mutableprotected

Definition at line 262 of file poisson_nitsche_interface.h.

◆ error_table

template<int dim, int spacedim = dim>

ParsedTools::ConvergenceTable PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::error_table

protected

Definition at line 265 of file poisson_nitsche_interface.h.

◆ data_out

template<int dim, int spacedim = dim>

ParsedTools::DataOut<spacedim, spacedim> PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::data_out

mutableprotected

Choosing as embedded space the square \([-.0.45,0.45]^2\) and as embedding space the square \([-1,1]^2\), with embedded value the function \(g(x,y)=1\), this is what we get.

Taking a manufactured smooth solution \(u=\sin(2 \pi x) \sin(2 \pi y)\), classical rates can be observed, as in the following table: cells dofs u_L2_norm u_Linfty_norm u_H1_norm 256 289 5.851e-02 - 8.125e-02 - 2.015e+00 - 1024 1089 1.436e-02 2.12 2.160e-02 2.00 1.007e+00 1.05 4096 4225 3.605e-03 2.04 5.519e-03 2.01 5.037e-01 1.02

Definition at line 283 of file poisson_nitsche_interface.h.

◆ console_level

template<int dim, int spacedim = dim>

unsigned int PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::console_level = 1

protected

Level of log verbosity.

Definition at line 289 of file poisson_nitsche_interface.h.

◆ penalty

template<int dim, int spacedim = dim>

double PDEs::Serial::PoissonNitscheInterface< dim, spacedim >::penalty = 100.0

protected

The penalty parameter which multiplies Nitsche's terms.

In this program it is defaulted to 100.0

Definition at line 299 of file poisson_nitsche_interface.h.

The documentation for this class was generated from the following files:

include/pdes/serial/poisson_nitsche_interface.h
source/pdes/serial/poisson_nitsche_interface.cc

Public Member Functions

Protected Member Functions

Protected Attributes

Additional Inherited Members

Detailed Description

template<int dim, int spacedim = dim> class PDEs::Serial::PoissonNitscheInterface< dim, spacedim >

Constructor & Destructor Documentation

◆ PoissonNitscheInterface()

Member Function Documentation

◆ run()

◆ generate_grids()

◆ setup_system()

◆ assemble_system()

◆ solve()

◆ output_results()

Member Data Documentation

◆ component_names

◆ grid_generator

◆ embedded_grid_generator

◆ grid_refinement

◆ space_triangulation

◆ embedded_triangulation

◆ space_cache

◆ embedded_cache

◆ cells_and_quads

◆ space_fe

◆ space_dh

◆ mapping

◆ space_constraints

◆ sparsity_pattern

◆ system_matrix

◆ solution

◆ system_rhs

◆ inverse_operator

◆ preconditioner

◆ constants

◆ forcing_term

◆ embedded_value

◆ nitsche_coefficient

◆ exact_solution

◆ boundary_conditions

◆ timer

◆ error_table

◆ data_out

◆ console_level

◆ penalty

template<int dim, int spacedim = dim>
class PDEs::Serial::PoissonNitscheInterface< dim, spacedim >