Numerical Methods for Partial Differential Equations​

This course offers a comprehensive exploration into the numerical solution of Partial Differential Equations (PDEs), with a special emphasis on Finite Element Methods (FEMs). 

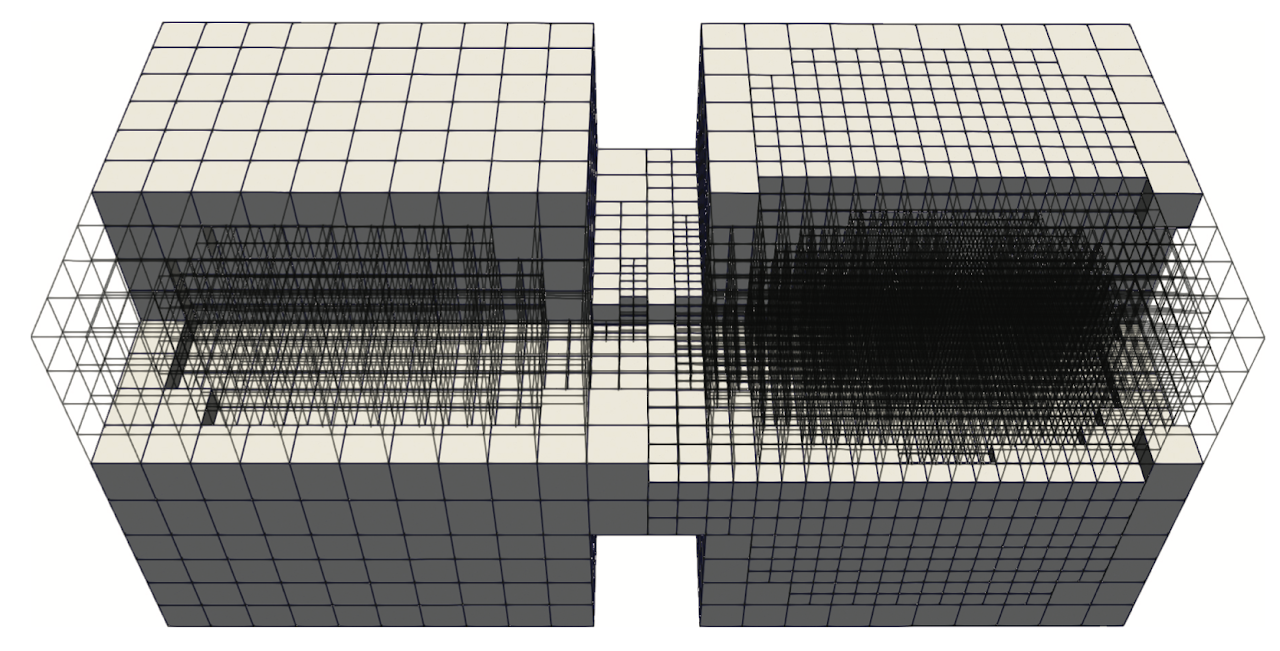
The curriculum explores the construction of Finite Element Spaces and polynomial approximation theory in Sobolev Spaces, to establish classical convergence theorems for elliptic problems. The course covers as well “variational crimes” and mixed methods, expanding the theory’s applicability to a wider range of PDEs. The theory is complemented with practice, using both front lectures and flipped classroom laboratories, working on implementations based on C++ using the deal.II library.

Key principles such as consistency, stability, convergence, and adaptivity will be examined in detail, offering guidelines for the selection and implementation of numerical methods suitable for the solution of a broad spectrum of partial differential equations.